Phylogenetics: MrBayes Lab

|
EEB 349: Phylogenetics |
| The goal of this lab exercise is to introduce you to the most important software for conducting Bayesian phylogenetic analyses, MrBayes. You will also learn how to use the program Tracer to analyze MrBayes' output. |
Contents
Download MrBayes and the data file
Download MrBayes
Download MrBayes from its MrBayes home page. MrBayes will unpack to form a folder containing several example NEXUS data files and the executable file (MrBayes3.1.2 on Mac, mrbayes.exe on Windows).
Download and save the data file
Save the contents of the file algaemb.nex to a file in the MrBayes folder. Important: unless you are a masochist, save the data file in the MrBayes folder so that MrBayes can easily find it!. This is the same 16S data you have used before (algae.nex), but the original file had to be changed to accommodate MrBayes' eccentricities. While MrBayes does a fair job of reading Nexus files, it chokes on certain constructs. The information about what I had to change in order to get it to work is in a comment at the top of the file (this might be helpful in converting other nexus files to work with MrBayes in the future).
Creating a MRBAYES block
The next step is to set up an MCMC analysis. There are three commands in particular that you will need to know about in order to set up a typical run: lset, prset and mcmc. The command mcmcp is identical to mcmc except that it does not actually start a run. For each of these commands you can obtain online information by typing help followed by the command name: for example, help prset. This may spew more information than will fit on your screen, however.
Create a MRBAYES block in your Nexus data file. MrBayes does not have a built-in editor, so you will need to use your favorite text editor to edit the algaemb.nex data file. Add the following at the very bottom of the file to begin creating the MRBAYES block:
begin mrbayes; end;
Add subsequent commands (described below) between the begin mrbayes; line and the end; line. Note that commands in MrBayes are (intentionally) similar to those in PAUP*, but the differences can be frustrating. For instance, lset ? in PAUP* gives you information about the current likelihood settings, but this does not work in MrBayes. Instead, you type help lset. Also, the lset command in MrBayes has many options not present in PAUP*, and vice versa. Get used to typing help followed by the name of a command in MrBayes to see what options are allowed for a particular command.
Specifying the prior on branch lengths
prset brlenspr=unconstrained:exp(10.0);
The above command specifies that branch lengths are to be unconstrained (i.e. a molecular clock is not assumed) and the prior distribution to be applied to each branch length is an exponential distribution with mean 1/10. Note that the value you specify for unconstrained:exp is the inverse of the mean.
Specifying the prior on the gamma shape parameter
prset shapepr=exp(1.0);
This command specifies an exponential distribution with mean 1.0 for the shape parameter of the gamma distribution we will use to model rate heterogeneity. Note that we have not yet told MrBayes that we wish to assume that substitution rates are variable - we will do that using the lset command below.
Specifying the prior on kappa
prset tratiopr=beta(1.0,1.0);
The command above says to use a Beta(1,1) distribution as the prior for the transition/transversion rate ratio. You may be thinking that it is a little strange to use a Beta distribution for a parameter that ranges from 0 to infinity, and if so you would be right! Allow me to explain as best I can. Recall that the kappa parameter is the ratio 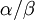 , where
, where 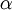 is the rate of transitions and
is the rate of transitions and 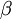 is the rate of transversions. Rather than allowing you to place a prior directly on the ratio
is the rate of transversions. Rather than allowing you to place a prior directly on the ratio 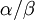 , which ranges from 0 to infinity, MrBayes asks you to instead place a joint (Beta) prior on
, which ranges from 0 to infinity, MrBayes asks you to instead place a joint (Beta) prior on 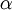 and
and 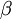 . Here,
. Here, 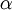 and
and 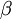 act like
act like  and
and 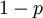 in the familiar coin flipping experiment. The reasoning behind this is esoteric, but is the same as the reasoning behind the (now commonplace) use of Dirichlet priors for the GTR relative rates, which is explained nicely in Zwickl and Holder (2004)[1].
in the familiar coin flipping experiment. The reasoning behind this is esoteric, but is the same as the reasoning behind the (now commonplace) use of Dirichlet priors for the GTR relative rates, which is explained nicely in Zwickl and Holder (2004)[1].
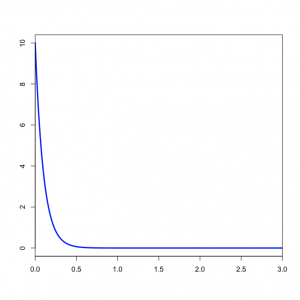
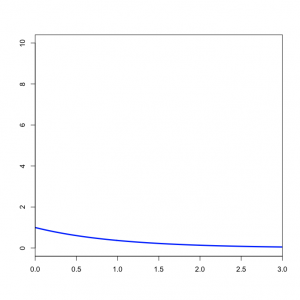
You might wonder what the Beta(1,1) distribution (figure on the left) implies about kappa. Transforming the Beta density into the density of 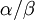 results in the plot on the right. This density for kappa is very close, but not identical, to an exponential(1) distribution. This is known as the Beta Prime distribution, and has support (0, infinity), which is appropriate for a ratio such as kappa. The Beta Prime distribution is somewhat peculiar, however, when both parameters are 1 (as they are in this case): in this case, the mean is not defined, which is to say that we cannot predict the mean of a sample of kappa values drawn from this distribution. It is not necessary for a prior distribution to have a well-defined mean, so this is OK.
results in the plot on the right. This density for kappa is very close, but not identical, to an exponential(1) distribution. This is known as the Beta Prime distribution, and has support (0, infinity), which is appropriate for a ratio such as kappa. The Beta Prime distribution is somewhat peculiar, however, when both parameters are 1 (as they are in this case): in this case, the mean is not defined, which is to say that we cannot predict the mean of a sample of kappa values drawn from this distribution. It is not necessary for a prior distribution to have a well-defined mean, so this is OK.
Specifying a prior on base frequencies
prset statefreqpr=dirichlet(1.0,1.0,1.0,1.0);
The above command states that a flat dirichlet distribution is to be used for base frequencies. The Dirichlet distribution is like the Beta distribution, except that it is applicable to combinations of parameters. Like the Beta distribution, the distribution is symmetrical if all the parameters of the distribution are equal, and the distribution is flat if all the parameters of the distribution are equal to 1.0. Using the command above specifies a flat Dirichlet prior, which says that any combination of base frequencies will be given equal prior weight. This means that (0.01, 0.99, 0.0, 0.0) is just as probable, a priori, as (0.25, 0.25, 0.25, 0.25). If you wanted base frequencies to not stray much from (0.25, 0.25, 0.25, 0.25), you could specify, say, statefreqpr=dirichlet(10.0,10.0,10.0,10.0) instead.
The lset command
lset nst=2 rates=gamma ngammacat=4;
We are finished setting priors now, so the command above finishes our specification of the model by telling MrBayes that we would like a 2-parameter substitution matrix (i.e. the rate matrix has only two substitution rates, the transition rate and the transversion rate). It also specifies that we would like rates to vary across sites according to a gamma distribution with 4 categories.
Specifying MCMC options
mcmcp ngen=10000 samplefreq=10 printfreq=100 nruns=1 nchains=3 startingtree=random savebrlens=yes;
The command above specifies most of the remaining details of the analysis.
ngen=10000 tells MrBayes that its robots should each take 10,000 steps. You should ordinarily use much larger values for ngen than this (the default is 1 million steps). We're keeping it small here because we do not have a lot of time and the purpose of this lab is to learn how to use MrBayes, not produce a publishable result. samplefreq=10 says to only save parameter values and the tree topology every 10 steps. printfreq=100 says that we would like a progress report every 100 steps.
nruns=1 says to just do one independent run. MrBayes performs two separate analyses by default.
nchains=3 says that we would like to have 2 heated chains running in addition to the cold chain.
startingtree=random means that we wish to begin from a random starting tree (as opposed to starting with a specific pre-determined tree topology).
Finally, savebrlens=yes tells MrBayes that we would like it to save branch lengths when it saves the sampled tree topologies.
Specifying an outgroup
outgroup Anacystis_nidulans;
This merely affects the display of trees. It says we want trees to be rooted between the taxon Anacystis_nidulans and everything else.
The autoclose command
set autoclose=yes;
This tells MrBayes that we will not want to continue the run beyond the 10,000 generations specified. If you leave this out, MrBayes will ask you whether you wish to continue running the chains after the specified number of generations is finished.
The final product
The mrbayes block at the bottom of your data file should now look like this:
begin mrbayes; prset brlenspr=unconstrained:exp(10.0); prset shapepr=exp(1.0); prset tratiopr=beta(1.0,1.0); prset statefreqpr=dirichlet(1.0,1.0,1.0,1.0); lset nst=2 rates=gamma ngammacat=4; mcmcp ngen=10000 samplefreq=10 printfreq=100 nruns=1 nchains=3 startingtree=random savebrlens=yes; outgroup Anacystis_nidulans; set autoclose=yes; end;
Running MrBayes and interpreting the results
Now save the file, start MrBayes by double-clicking on its icon, and once it starts, type
exe algaemb.nex
at the MrBayes to load the data. Then type
mcmc
This command starts the run. While MrBayes runs, it shows one-line progress reports. The first column is the step number. The next three columns show the log-likelihoods of the separate chains that are running, with the cold chain indicated by square brackets rather than parentheses. The last complete column is a prediction of the time remaining until the run completes. The columns consisting of only -- are simply separators, they have no meaning.
- Do you see evidence that the 3 chains are swapping with each other?
When the run has finished, MrBayes will report various statistics about the run, such as the percentage of time it was able to accept proposed changes of various sorts. These percentages should, ideally, all be between about 20% and 40%, but as long as they are not extreme (e.g. 1% or 99%) then things went well.
- What explanation could you offer if the acceptance rate was very low, e.g. 1%?
- What explanation could you offer if the acceptance rate was very high, e.g. 99%?
The section entitled "Chain swap information" reports the number of times the cold chain attempted to swap with the heated chain (lower left) and the proportion of time such attempts were successful (upper right). The total number of attempted swaps should be the same as the number of generations, i.e. 10,000.
Note the section of the output labeled Acceptance rates for moves in the "cold" chain. This gives the proportion of the time that proposals for various parameters were accepted:
Acceptance rates for the moves in the "cold" chain:
With prob. Chain accepted changes to
30.70 % param. 1 (tratio) with Dirichlet proposal
19.46 % param. 2 (state frequencies) with Dirichlet proposal
49.38 % param. 3 (gamma shape) with multiplier
18.18 % param. 4 (topology and branch lengths) with extending TBR
20.54 % param. 4 (topology and branch lengths) with LOCAL
In the above table, 49.38% of proposals to change the gamma shape parameter were accepted. This makes it sounds as if the gamma shape parameter was changed quite often, but to get the full picture, you need to scroll up to the beginning of the output and examine this section:
The MCMC sampler will use the following moves:
With prob. Chain will change
4.35 % param. 1 (tratio) with Dirichlet proposal
4.35 % param. 2 (state frequencies) with Dirichlet proposal
4.35 % param. 3 (gamma shape) with multiplier
65.22 % param. 4 (topology and branch lengths) with extending TBR
21.74 % param. 4 (topology and branch lengths) with LOCAL
This says that an attempt to change the gamma shape parameter will only be made in 4.35% of the iterations. That means, out of 10000 iterations (called generations by MrBayes), only 435 attempts were made to change the gamma shape parameter, and 49.38% of those, or 215, were accepted. If you were keenly interested in the posterior distribution of the gamma shape parameter, you would probably want to base it on more than 215 values.
This brings up a couple of important points. First, in each iteration, MrBayes chooses a move at random to try. Each move is associated with a "proposal rate". The proposal rates can be listed using the props command (see below for how to run this command). Using the props command shows the following list of all possible moves (many of which are not used in any particular analysis). I've made the five moves listed above bold and blue- for now just note the proposal rates for these five moves:
1 -- Change (amino acid model) randomly
proposal rate: 1.000
2 -- Change (correlation of adgamma) with sliding window
proposal rate: 1.000
sliding window size: 0.500
3 -- Change (symmetric Dirichlet/Beta) with multiplier
proposal rate: 1.000
multiplier tuning parameter (lambda): 0.811
4 -- Change (branch lengths) with multiplier
proposal rate: 0.000
multiplier tuning parameter (lambda): 1.386
5 -- Change (extinction rate) with sliding window
proposal rate: 1.000
sliding window size: 1.000
6 -- Change (extinction rate) with multiplier
proposal rate: 0.000
multiplier tuning parameter (lambda): 0.811
7 -- Change (topology and branch lengths) with extending SPR (clock)
proposal rate: 10.000
extension probability: 0.700
8 -- Change (topology and branch lengths) with extending TBR
proposal rate: 15.000
extension probability: 0.800
multiplier tuning parameter (lambda): 0.940
9 -- Change (gamma shape) with multiplier
proposal rate: 1.000
multiplier tuning parameter (lambda): 0.811
10 -- Change (population growth) with sliding window
proposal rate: 1.000
sliding window size: 5.000
11 -- Change (topology and branch lengths) with LOCAL
proposal rate: 5.000
multiplier tuning parameter (lambda): 0.191
12 -- Change (topology and branch lengths) with clock-constrained LOCAL*
proposal rate: 0.000
13 -- Change (parsimony topology) with NNI
proposal rate: 10.000
14 -- Change (topology and branch lengths) with NNI (heterogen.)
proposal rate: 15.000
multiplier tuning parameter (lambda): 0.940
15 -- Change (branch lengths) with nodeslider
proposal rate: 0.000
multiplier tuning parameter (lambda): 0.191
16 -- Change (branch lengths) with node slider (clock)
proposal rate: 7.000
window size: 0.050
17 -- Change (omega) with sliding window
proposal rate: 1.000
sliding window size: 1.000
18 -- Change (omega) with multiplier
proposal rate: 0.000
multiplier tuning parameter (lambda): 0.811
19 -- Change (M10 beta distribution) with multiplier
proposal rate: 1.000
multiplier tuning parameter (lambda): 0.191
20 -- Change (omega cat. freqs.) with sliding window
proposal rate: 1.000
sliding window size: 0.500
21 -- Change (M10 gamma distribution) with multiplier
proposal rate: 1.000
multiplier tuning parameter (lambda): 0.191
22 -- Change (omega 2) with sliding window
proposal rate: 1.000
sliding window size: 0.500
23 -- Change (omega 3/+) with sliding window
proposal rate: 1.000
sliding window size: 1.000
24 -- Change (omega 1/-) with sliding window
proposal rate: 1.000
sliding window size: 0.100
25 -- Change (prop. invar. sites) with sliding window
proposal rate: 1.000
sliding window size: 0.100
26 -- Change (rate multiplier) with Dirichlet proposal
proposal rate: 1.000
Dirichlet parameter: 500.000
27 -- Change (revmat) with Dirichlet proposal
proposal rate: 1.000
Dirichlet parameter: 500.000
28 -- Change (speciation rate) with sliding window
proposal rate: 1.000
sliding window size: 1.000
29 -- Change (speciation rate) with multiplier
proposal rate: 0.000
multiplier tuning parameter (lambda): 0.811
30 -- Change (state frequencies) with Dirichlet proposal
proposal rate: 1.000
Dirichlet parameter: 300.000
31 -- Change (symDir multistatefreqs) with Dirichlet proposal
proposal rate: 5.000
Dirichlet parameter (alphaPi): 50.000
32 -- Change (covarion switch rates) with sliding window
proposal rate: 1.000
sliding window size: 1.000
33 -- Change (covarion switch rate) with multiplier
proposal rate: 0.000
multiplier tuning parameter (lambda): 0.811
34 -- Change (coalescence parameter) with sliding window
proposal rate: 1.000
sliding window size: 1.000
35 -- Change (tratio) with Dirichlet proposal
proposal rate: 1.000
beta parameter: 50.000
36 -- Change (tree height) with multiplier
proposal rate: 7.000
multiplier tuning parameter (lambda): 0.098
Summing the five proposal rates yields 1+1+1+5+15=23. To get the probability of using one of these moves in any particular iteration, MrBayes divides the proposal rate for the move by this sum. Thus, kappa (which MrBayes calls tratio), state frequencies and the gamma shape parameter will all be chosen with probability 1/23 = 0.0435, i.e. they will each be updated in about 4.35% of the iterations.
Second, note that MrBayes places a lot of emphasis on modifying the tree topology and branch lengths (87% of proposals), but puts little effort (13%) into updating other model parameters. You can change the percent effort for a particular move using the props command. For example, to increase the effort devoted to updating the gamma shape parameter, enter props at the MrBayes prompt, then the number of this proposal (9), then type a number greater than 1 for the proposal rate (e.g. 5). At the same time, you get an opportunity to change the tuning parameter for this move; press return to keep the current tuning parameter value. Press 0 now to exit the props command and type mcmc to run another analysis. Note now the gamma shape parameter will now be modified in 18.52% of iterations:
With prob. Chain will change 3.70 % param. 1 (tratio) with Dirichlet proposal 3.70 % param. 2 (state frequencies) with Dirichlet proposal 18.52 % param. 3 (gamma shape) with multiplier 55.56 % param. 4 (topology and branch lengths) with extending TBR 18.52 % param. 4 (topology and branch lengths) with LOCAL
The sump command
MrBayes saves information in several files. Only two of these will concern us today. One of them will be called algaemb.nex.p. This is the file in which the sampled parameter values were saved. This file is saved in tab-delimited format so that it is easy to import into a spreadsheet program such as Excel. We will examine this file graphically in a moment, but first let's get MrBayes to summarize its contents for us.
At the MrBayes prompt, type the command sump. This will generate a crude graph showing the log-likelihood as a function of time. Note that the log-likelihood starts out low on the left (you started from a random tree, remember), then quickly climbs to a constant value.
Below the graph, MrBayes provides the arithmetic mean and harmonic mean of the marginal likelihood. The harmonic mean is used in estimating Bayes factors, which are in turn useful for deciding which among different models fits the data best on average. We will talk about how to use this value in lecture, where you will also get some warnings about Bayes factors calculated in this way.
The table at the end is quite useful. It shows the posterior mean, median, variance and 95% credible interval for each parameter in your model based on the samples taken during the run. The credible interval shows the range of values of a parameter that account for the middle 95% of its marginal posterior distribution. If the credible interval for kappa is 3.8 to 6.8, then you can say that there is a 95% chance that kappa is between 3.8 and 6.8 given your data (and of course the model). The parameter TL represents the sum of all the branch lengths. Rather than reported every branch length individually, MrBayes just keeps track of their sum.
The sumt command
Now type the command sumt. This will summarize the trees that have been saved in the file algaemb.nex.t.
The output of this command includes a bipartition (=split) table, showing posterior probabilities for every split found in any tree sampled during the run. After the bipartition table is shown a majority-rule consensus tree containing all splits that had posterior probability 0.5 or above.
If you chose to save branch lengths (and we did), MrBayes shows a second tree in which each branch is displayed in such a way that branch lengths are proportional to their posterior mean. MrBayes keeps a running sum of the branch lengths for particular splits it finds in trees as it reads the file algaemb.nex.t. Before displaying this tree, it divides the sum for each split by the total number of times it encountered the split to get a simple average branch length for each split. It then draws the tree so that branch lengths are proportional to these mean branch lengths.
Finally, the last thing the sumt command does is tell you how many tree topologies are in credible sets of various sizes. For example, in my run, it said that the 99% credible set contained 18 trees. What does this tell us? MrBayes orders tree topologies from most frequent to least frequent (where frequency refers to the number of times they appear in algaemb.nex.t). To construct the 99% credible set of trees, it begins by adding the most frequent tree to the set. If that tree accounts for 99% or more of the posterior probability (i.e. at least 99% of all the trees in the algaemb.nex.t file have this topology), then MrBayes would say that the 99% credible set contains 1 tree. If the most frequent tree topology was not that frequent, then MrBayes would add the next most frequent tree topology to the set. If the combined posterior probability of both trees was at least 0.99, it would say that the 99% credible set contains 2 trees. In our case, it had to add the top 18 trees to get the total posterior probability up to 99%.
Type quit (or just q), to quit MrBayes now.
Using Tracer to summarize MCMC results
The Java program Tracer is very useful for summarizing the results of Bayesian phylogenetic analyses. Tracer was written to accompany the program Beast, but it works well with the output file produced by MrBayes as well.
After starting Tracer, choose File > Import... to choose a parameter sample file to display. Select the algaemb.nex.p in your working folder, then click the Open button to read it.
You should now see 8 rows of values in the table labeled Traces on the left side of the main window. The first row (LnL) is selected by default, and Tracer shows a histogram of log-likelihood values on the right, with summary statistics above the histogram.
A histogram is perhaps not the most useful plot to make with the LnL values. Click the Trace tab to see a trace plot (plot of the log-likelihood through time).
Tracer determines the burn-in period using an undocumented algorithm. You may wish to be more conservative than Tracer. Opinions vary about burn-in. Some Bayesians feel it is important to exclude the first few samples because it is obvious that the chains have not reached stationarity at this point. Other Bayesians feel that if you are worried about the effect of the earliest samples, then you definitely have not run your chains long enough! You might be interested in reading Charlie Geyer's rant on burn-in some time.
Click the Estimates tab again at the top, then click the row labeled kappa on the left.
- What is the posterior mean of kappa?
- What is the 95% credible interval for kappa?
Click the row labeled alpha on the left. This is the shape parameter of the gamma distribution governing rates across sites.
- What is the posterior mean of alpha?
- What is the 95% credible interval for alpha?
- Is there rate heterogeneity among sites, or are all sites evolving at nearly the same rate?
Click on the row labeled TL on the left (the Tree Length).
- What is the posterior mean tree length?
- What is the mean edge length? (Hint: divide the tree length by the number of edges, which is 2n-3 if n is the number of taxa.)
Running MrBayes with no data
Why would you want to run MrBayes with no data? Here's a possible reason. You discover by reading the text that results from typing help prset that MrBayes assumes, by default, the following branch length prior: exp(10). What does the 10 mean here? Is this an exponential distribution with mean 10 or is 10 the so-called "rate" parameter (a common way to parameterize the exponential distribution)? If 10 is correctly interpreted as the rate parameter, then the mean of the distribution is 1/rate, or 0.1. Even good documentation such as that provided for MrBayes does not explicitly spell out everything you might want to know, but running MrBayes without data can provide answers, at least to questions concerning prior distributions.
Also, it is not possible to place prior distributions directly on some quantities of interest. For example, while you can specify a flat prior on topologies, it is not possible to place a prior on a particular split you are interested in. This is because the prior distribution of splits is induced by the prior you place on topologies. Running a Bayesian MCMC program without data is a good way to make sure you know what priors you are actually placing on the quantities of interest. Even if you think you know, running without data provides a good sanity check.
If there is no information in the data, the posterior distribution equals the prior distribution. An MCMC analysis in such cases provides an approximation of the prior.
Execute the file blank.nex in MrBayes. Here is what this file looks like (use your favorite text editor to create this file in the MrBayes directory):
#nexus begin data; dimensions ntax=4 nchar=1; format datatype=dna missing=? gap=-; matrix A ? B ? C ? D ? ; end; begin mrbayes; set autoclose=yes; prset brlenspr=unconstrained:exp(10.0); prset tratiopr=beta(1.0,1.0); prset statefreqpr=Dirichlet(1.0,1.0,1.0,1.0); prset shapepr=exp(1.0); lset nst=2 rates=gamma ngammacat=4; mcmcp ngen=1000000 samplefreq=100 printfreq=10000 nruns=1 nchains=1; end;
Note that the data matrix consists of just one character, and that character declares that data are missing for all taxa!
Type mcmc to perform the analysis. Because calculation of the likelihood is the most time-consuming part of a Bayesian analysis, this analysis will go quickly because the likelihood for just one site takes almost no time to compute.
- Consulting Bayes' formula, what value of the likelihood would cause the posterior to equal the prior?
- Is this the value that MrBayes reports for the log-likelihood in this case?
Checking the shape parameter prior
Import the output file blank.nex.p in Tracer. Look first at the histogram of alpha, the shape parameter of the gamma distribution.
- What is the mean you expected for alpha based on the prset shapepr=exp(1.0) command in the blank.nex file?
- What is the posterior mean actually estimated by MrBayes (and presented by Tracer)?
- An exponential distribution always starts high and approaches zero as you move to the right along the x-axis. The highest point of the exponential density function is 1/mean. If you look at the approximated density plot (click on the Marginal Density tab), does it appear to approach 1/mean at the value alpha=0.0?
Checking the branch length prior
Now look at the histogram of TL, the tree length.
- What is the posterior mean of TL, as reported by Tracer?
- What value did you expect based on the prset brlenspr=unconstrained:exp(10) command?
- Does the approximated posterior distribution of TL appear to be an exponential distribution?
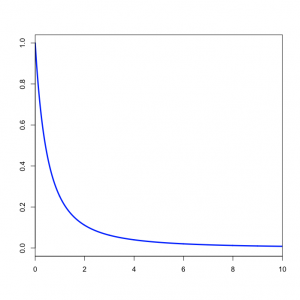
The second and third questions are a bit tricky, so I'll just give you the explanation. Please make sure this explanation makes sense to you, however, and ask us to explain further if it doesn't make sense. We told MrBayes to place an exponential prior with mean 0.1 on each branch. There are 5 branches in a 4-taxon, unrooted tree. Thus, 5 times 0.1 equals 0.5, which should be close to the posterior mean you obtained for TL. That part is fairly straightforward.
The marginal distribution of TL does not look at all like an exponential distribution, despite the fact that TL should be the sum of 5 exponential distributions. It turns out that the sum of  independent Exponential(
independent Exponential(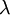 ) distributions is a Gamma(
) distributions is a Gamma( ,
, 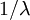 ) distribution. In our case the tree length distribution is a sum of 5 independent Exponential(10) distributions, which equals a Gamma(5, 0.1) distribution. Such a Gamma distribution would have a mean of 0.5 and a peak (mode) at 0.4. If you want to visualize this, fire up R and type the following commands:
) distribution. In our case the tree length distribution is a sum of 5 independent Exponential(10) distributions, which equals a Gamma(5, 0.1) distribution. Such a Gamma distribution would have a mean of 0.5 and a peak (mode) at 0.4. If you want to visualize this, fire up R and type the following commands:
x <- seq(0, 2, .001) y <- dgamma(x, shape=5, scale=0.1) plot(x, y, type="l")
- How does the Gamma(5, 0.1) density compare to the distribution of TL as shown by Tracer? (Be sure to click the "Marginal Density" tab in Tracer)
Other output files produced by MrBayes
That's it for the lab today. You can look at plots of the other parameters if you like. You should also spend some time opening the other output files MrBayes produces in a text editor to make sure you understand what information is saved in these files. Note that some of MrBayes' output files are actually Nexus tree files, which you can open in FigTree. For example, algaemb.nex.con contains the consensus tree from the Bayesian analysis, and algaemb.nex.t contains the sampled trees. The file algaemb.nex.trprobs contains all distinct tree topologies, sorted from highest to lowest posterior probability.
Just for fun
Do this section only if you have time. Tree Set Viz is a program that uses multidimensional scaling to flatten the multidimensional space of tree topologies into just two dimensions. Before you get too excited, just think about some familiar three dimensional objects (e.g. squirrels) and note how much is lost when they are flattened down to just two dimensions. So, let's use Tree Set Viz to flatten out the sample of trees produced by MrBayes as it ran.
Tree Set Viz is not a standalone program. It is a module in the Java program Mesquite. Thus, you will probably need to install both Mesquite and Tree Set Viz. Another problem is that Mesquite is evolving much faster than Tree Set Viz, so as of this writing (March 24, 2009) you need to install an old version of Mesquite if we want to use Tree Set Viz.
Installing Mesquite 1.12 under MacOSX
Download Mesquite 1.12 from the http://mesquiteproject.org/mesquite1.12/mesquiteDownload/ (don't use the main Mesquite project download site, because then you will get version 2.6 (or higher), which is incompatible with Tree Set Viz). Open the mesquite.dmg file that you downloaded and then drag the Mesquite Folder therein to your Applications folder. To start Mesquite, find Mesquite OSX.app in Applications/Mesquite Folder and double-click it. (Note that the .app part of the name may be hidden; to unhide file extensions, check "Show all file extensions" in your Finder preferences.)Installing Mesquite 1.12 under Windows
Download Mesquite 1.12 from the http://mesquiteproject.org/mesquite1.12/mesquiteDownload/ (don't use the main Mesquite project download site, because then you will get version 2.6 (or higher), which is incompatible with Tree Set Viz). Run the MesquiteInstaller.exe file that you downloaded. I recommend unchecking the box labeled "Make Mesquite the default application for opening Nexus files" when it appears. This will create a folder named Mesquite Folder inside your Program Files directory. To start Mesquite, find Mesquite.exe in C:\Program Files\Mesquite Folder and double-click it. (Note that the .exe part of the name may be hidden; to unhide file extensions, uncheck "Hide extensions for known file types" in the View tab of Folder Options, which on Vista is a control panel visible in classic view.)Installing Tree Set Viz module
Tree Set Viz is a Mesquite module that tries to depict the tree topologies in a sample of trees in a two-dimensional space using multidimensional scaling. Download the Java class files for Mesquite 1.05 and higher. The downloaded file will be named treecomp_classfiles_20041111.tar.gz. Uncompressing (double-click on the Mac, use your favorite unzip program on Windows) this file will produce a folder named treecomp. This entire folder (not just its contents) should be moved to Applications/Mequite Folder/mesquite. Mesquite must be restarted for the presence of this module to be detected.
Viewing your treefile
Follow these directions carefully (do not wander from the path, or you will be lost in Mesquiteshire and never find your way back again!):
- Start Mesquite
- Click OK to the "Welcome to Mesquite" message box that appears
- After Mesquite stops loading modules, choose File, then Open File... from the main Mesquite menu
- Locate and select the tree file from your MrBayes run (e.g. algaemb.nex.t), then click the Open button to open it
- Ignore the warning about missing taxa block (Mesquite will make up one that works)
- Select the "Tree Set Visualization 2.1" menu item from the "Taxa&Trees" menu
- Select "Stored Trees" and press OK
- Select "Robinson-Foulds Tree Difference" and press the OK button
- After a minute, you should be looking at a field of stars in the night sky. Click the "Tree Coloring" checkbox and then, when prompted, choose the parameter file (e.g. algaemb.nex.p) that corresponds to the tree file you opened
- Most of the "stars" (each dot represents a tree topology from the file) will now be colored red. Use the scale on the right to see what the colors mean. The few blue or green trees that are scattered around are part of the burn-in period when very poor trees were being visited.
- Click the "Start MDS" button to begin the flattening process. The MDS procedure tries to move trees around in the 2D space so that the stress is minimized. The stress is a measure of the difference between the pairwise tree-to-tree distances and the corresponding Euclidean distance in the 2D space. If the stress could be reduced to zero, it would mean that the original space was actually two-dimensional.
- After letting MDS run for awhile, stop it using the "Stop MDS" button and press the "Animate Tree Order" button. This causes Tree Set Viz to display the dots corresponding to tree topologies in the order in which they were encountered in the tree file. Note that the first few dots are invariably the blue and green ones, which makes sense because MrBayes started from a random tree. Also note that dots adjacent in time are also fairly close in 2D space. That's because MrBayes' robot proposes steps in tree space that are not too far away from the current location. This effect is more pronounced if you tell MrBayes to save the tree corresponding to every generation (mcmcp samplefreq=1).
- Now use your mouse to select a group of dots. Tree Set Viz will pop up a window showing the strict consensus tree for the topologies you selected. If that ain't cool, I don't know what is!
Literature Cited
- ↑ Zwickl, D., and Holder, M. T. 2004. Model parameterization, prior distributions, and the general time-reversible model in Bayesian phylogenetics. Systematic Biology 53(6):877–888