Difference between revisions of "Phylogenetics: Morphology and Partitioning in MrBayes"
Paul Lewis (Talk | contribs) (→Estimating the marginal likelihood using the stepping-stone method) |
Paul Lewis (Talk | contribs) (→Estimating the marginal likelihood using the stepping-stone method) |
||
| Line 262: | Line 262: | ||
MrBayes will, in our case, divide the 11000 samples (1100000 generations divided by 100 generations/sample) by 11 steps to yield 1000 samples per step. This is a little confusing because we specified <tt>nsteps=10</tt>, not <tt>nsteps=11</tt>. By default, MrBayes uses the first step as burnin, so you need to specify <tt>ngen</tt> and <tt>samplefreq</tt> in such a way that you get the desired number of samples per step. The formula is ngen = (nsteps+1)*(samplefreq)*(samples/step). In our case, ngen = (10+1)*(100)*(1000) = 1100000. | MrBayes will, in our case, divide the 11000 samples (1100000 generations divided by 100 generations/sample) by 11 steps to yield 1000 samples per step. This is a little confusing because we specified <tt>nsteps=10</tt>, not <tt>nsteps=11</tt>. By default, MrBayes uses the first step as burnin, so you need to specify <tt>ngen</tt> and <tt>samplefreq</tt> in such a way that you get the desired number of samples per step. The formula is ngen = (nsteps+1)*(samplefreq)*(samples/step). In our case, ngen = (10+1)*(100)*(1000) = 1100000. | ||
| + | === Spacing the stepping stones === | ||
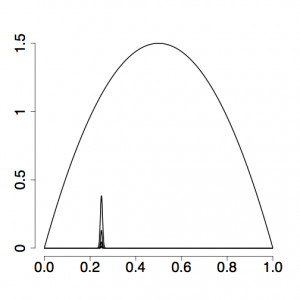
[[File:Alpha-1.0.png|thumb|right|Evenly spaced powers (here, 0.0, 0.2, 0.4, 0.6, 0.8, 1.0) result in a big gap between the prior and the next power posterior density]] | [[File:Alpha-1.0.png|thumb|right|Evenly spaced powers (here, 0.0, 0.2, 0.4, 0.6, 0.8, 1.0) result in a big gap between the prior and the next power posterior density]] | ||
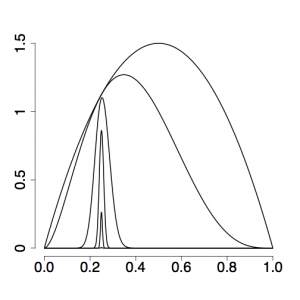
[[File:Alpha-0.17.png|thumb|right|A strongly skewed spacing of powers (here, 0.0, 0.000077, 0.0046, 0.050, 0.27, 1.0) result in a more even spacing of power posterior densities (and better estimates)]] | [[File:Alpha-0.17.png|thumb|right|A strongly skewed spacing of powers (here, 0.0, 0.000077, 0.0046, 0.050, 0.27, 1.0) result in a more even spacing of power posterior densities (and better estimates)]] | ||
The setting <tt>alpha=0.3</tt> has to do with how evenly spaced the stepping-stones are placed in the stream: if alpha were set to 1, the beta values used to modify the likelihood would all be the same distance apart. This does not translate into evenly-spaced stepping stones however, and setting alpha to be smaller than 1 usually results in more evenly spaced stones and thus more accurate estimates of ratios close to the prior end of the spectrum. | The setting <tt>alpha=0.3</tt> has to do with how evenly spaced the stepping-stones are placed in the stream: if alpha were set to 1, the beta values used to modify the likelihood would all be the same distance apart. This does not translate into evenly-spaced stepping stones however, and setting alpha to be smaller than 1 usually results in more evenly spaced stones and thus more accurate estimates of ratios close to the prior end of the spectrum. | ||
| + | === Interpreting the results === | ||
Once the run finishes, try to answer the following questions based on what you find in the <tt>outout.txt</tt> file: | Once the run finishes, try to answer the following questions based on what you find in the <tt>outout.txt</tt> file: | ||
<div style="background-color: #ccccff"> | <div style="background-color: #ccccff"> | ||
Revision as of 17:06, 10 March 2016

|
EEB 349: Phylogenetics |
| The goal of this lab is to learn how to analyze discrete morphological character data in MrBayes, to learn how to combine morphological with molecular data in a partitioned analysis in which each data type is assigned an appropriate model of evolution, and learn how to estimate the marginal likelihood of a model for purposes of model comparison and selection. |
Contents
- 1 The Nylander et al. study
- 2 Downloading the data file
- 3 Creating a command file
- 4 Starting a log file
- 5 Reducing the size of the data set
- 6 Creating a data partition
- 7 Specifying a model for the morphological data
- 8 Specifying a model for the 18S and COI data
- 9 Specifying branch length and gamma shape priors
- 10 Unlinking parameters
- 11 Finishing the MrBayes block
- 12 Running MrBayes on the cluster
- 13 Analyzing the output
- 14 Using the marginal likelihood to choose a model
- 15 Estimating the marginal likelihood using the stepping-stone method
- 16 Challenge
- 17 That's it for today
The Nylander et al. study
The data for this lab comes from a paper by Nylander et al. (2004) that has already become a landmark study in combining data within a Bayesian framework. The full citation is:
Nylander, J., F. Ronquist, J. P. Huelsenbeck, and J. Nieves-Aldrey. 2004. Bayesian phylogenetic analysis of combined data. Systematic Biology 53:47-67
If you have access, you can download the pdf of this paper.
Downloading the data file
The data from the paper is available from TreeBase. While you can download a nexus file containing all the data (search by Study Accession number for 1070 or by Author for Nylander), you will have trouble executing this file in MrBayes data file due to the use of CHARACTER blocks rather than DATA blocks, so I have done the transformation for you. Download the file by clicking here and save a copy to your local hard drive. This nylander.nex data file contains three of the five data sets analyzed by Nylander et al. (2004).
Creating a command file
Rather than adding a MRBAYES block to the data file, create a separate file (on your local computer) named go.nex that contains a MRBAYES block:
#nexus begin mrbayes; exe nylander.nex; charset morph = 1-166; charset 18S = 167-1320; charset COI = 1321-2397; end;
The first line of the MRBAYES block executes the data file nylander.nex. Each of the last three lines defines a charset, a meaningful set of characters. Each charset identifies one of the sources of data used in the Nylander et al. (2004) study. The first charset is named morph. While you can use any name you like to identify charsets, this name is appropriate because these are the discrete morphological characters. The second charset is named 18S because it contains 18S rRNA gene sequences. The third charset is named COI. This is a protein-coding gene in the mitochondrion that encodes part of the electron transport chain.
In this lab, you will build on this MRBAYES block, but be sure to keep the three charset lines above any other commands you add. Eventually you will perform an analysis on the cluster, but keep working on your own laptop until you have built the entire MRBAYES block.
Starting a log file
It is always a good idea to start a log file so that you can review the output produced by MrBayes at a later time. Add the following line to your MRBAYES block (after the charset definitions:
log start file=output.txt replace;
Here, I've named my log file output.txt and instructed MrBayes to replace this file without asking if it already exists.
Reducing the size of the data set
In order to have time for an analysis during the lab period, we will need to delete some taxa:
delete 1-11 19-21 26-32;
In addition, three morphological characters seem to cause problems for some models, so we will exclude these three characters:
exclude 29 56 58;
Creating a data partition
Your next task is to tell MrBayes how to partition the data. Used as a verb, partition means to erect walls or dividers. The correct term for the data between two partitions (i.e. dividers) is subset, but data subsets are often, confusingly, also called partitions! Even more confusing, the entire collection of subsets is known as a partition! Add the following lines to the end of your MRBAYES block to tell MrBayes that you want each of the 3 defined charsets to be a separate component (subset) of the partition:
partition mine = 3:morph,18S,COI;
The first number (3) is the number of subsets composing the partition. The name by which the partition is known in MrBayes is up to you: here I've chosen the name "mine".
Just defining a partition is not enough to get MrBayes to use it! You must tell MrBayes that you want to use the partition named "mine". This seems a little redundant, but the idea is that you can set up several different partitions and then easily turn them on or off simply by changing the partition named in the set command:
set partition=mine;
Specifying a model for the morphological data
The main reason for creating a partition is so that we can apply a different model to each subset. The first subset corresponds to the morph charset, so we need to apply a model appropriate to morphology to this subset.
The lset command
For each subset, you will create an lset and prset command. At the end of your existing mrbayes block, type in this lset command:
lset applyto=(1) coding=variable;
The applyto=(1) statement says that these settings apply only to the first (1) subset. The coding=variable statement instructs MrBayes to make the likelihood conditional on character variability, rather than the ordinary likelihood, which assumes that there will be an appropriate number of constant characters present.
The prset command
Now, we need to specify the priors for the parameters in the morphology model. The morphology model we are using is quite simple, so the only parameters are really just the branch lengths and the state frequencies.
We will use a simple symmetric model in which the frequency of each state is equal. The state frequencies are parameters that are present in the likelihood function. MrBayes allows you to assume that state frequencies follow a discrete Dirichlet distribution, much like relative rates are assumed to follow a discrete Gamma distribution in the "G" models of among-site rate heterogeneity. Note that if a character has only two states (e.g. 0 = absent and 1 = present), this discrete Dirichlet distribution is equivalent to a discrete Beta distribution. To force the state frequencies to be equal, the Dirichlet density should be a spike concentrated right at the value 1/(number of states). To specify this, set symdirihyperpr to fixed(infinity):
prset applyto=(1) symdirihyperpr=fixed(infinity) ratepr=variable;
You may be curious about the ratepr=variable statement. All data subsets will be using the same branch lengths, and because morphological characters are probably evolving at a different rate than DNA sequences, this statement causes MrBayes to give this subset its own relative rate. If the estimated value of this parameter ends up being 1.5, it means that the morphological characters evolve about one and a half times faster than the average character/site in the entire data set. The average substitution rate is what is reflected in the estimated branch lengths. It is always a good idea to include the ratepr=variable statement in each subset of a partitioned model when using MrBayes.
Specifying a model for the 18S and COI data
For the 18S sequences, ideally we would use a secondary structure model, but unfortunately I don't know which sites form stems and loops for these data. Thus, we will have to make do with using a standard DNA sequence model (the GTR+I+G model) for this subset. For the COI data, we would (again, in an ideal world) specify a codon model because this is a protein-coding gene. However, we don't have the time in a 2 hour lab to allow a codon model to run to convergence, so we will also be applying the standard GTR+I+G model to the COI data. We will, however, allow the 18S and COI to occupy different subsets of the partition so that they can have different relative rates of substitution.
The lset command
The lset command is similar to ones you have used before with MrBayes:
lset applyto=(2,3) nst=6 rates=invgamma;
The nst=6 tells MrBayes to use a 6-substitution-rate model (i.e. the GTR model) and the rates=invgamma part says to add invariable sites and discrete gamma rate heterogeneity onto the GTR base model. The applyto=(2,3) statement means that the remainder of the lset command only applies to the second (18S) and third (COI) subsets.
The prset command
Priors need to be specified for all the parameters of the GTR+I+G model except branch lengths and the gamma shape parameter. Because these (branch length and gamma shape priors) are being applied to all subsets, we'll specify these later.
prset applyto=(2,3) revmatpr=dirichlet(1,2,1,1,2,1) statefreqpr=dirichlet(2,2,2,2) pinvarpr=uniform(0,1) ratepr=variable;
This specifies a Dirichlet(1,2,1,1,2,1) prior for the 6 GTR relative substitution rate parameters. This prior is not flat, but it also is not very informative: it specifies a slight preference for transitions over transversions. For the base frequencies, we're specifying a vague Dirichlet(2,2,2,2) prior. Again, slightly informative, attaching very weak rubber bands to each relative base frequency, keeping the relative frequencies from straying too far from 0.25. The pinvarpr=uniform(0,1) applies a flat, uniform prior to the pinvar parameter. The applyto=(2,3) statement applies its prior settings to the second (18S data) and third (COI) data subsets. The last ratepr=variable statement in each case ensures that each subset will have a relative rate parameter that allows it to evolve at different rate (potentially) than other subsets.
Specifying branch length and gamma shape priors
The branch length and gamma shape priors apply to all subsets, so we can specify them like this:
prset applyto=(all) brlenspr=unconstrained:exponential(1.0) shapepr=exponential(1.0);
This says to apply an exponential distribution with mean 1 to all branch lengths and to all shape parameters.
Unlinking parameters
By default, MrBayes tries to create the simplest model possible. If you have specified the same model parameters (and the same priors) for more than one subset, MrBayes will "link" these parameters across subsets. This means that it will assume that the values of these linked parameters apply to all subsets involved in the linking. If you want the gamma shape parameter (for example) to take on potentially different values for the morphology, 18S and COI subsets, you have to make sure MrBayes does not automatically link the shape parameter across all three subsets.
unlink shape=(all) statefreq=(all) revmat=(all);
The above command ensures that different values will be used for the shape parameter, state frequencies and GTR relative rates for all data subsets.
Finishing the MrBayes block
Finish off the MrBayes block by adding mcmc, sump commands and a quit command as follows:
mcmc ngen=1000000 samplefreq=1000 printfreq=10000 nchains=1 nruns=1; sump; quit;
This says to run a single Markov chain for 1,000,000 generations, saving a sample of the tree and model parameters every 1000 generations and showing progress every 10000 generations. Ordinarily, it would be a good idea to let MrBayes use the default values for nchains and nruns (4 and 2, respectively), but I am skimping here due to the time constraints imposed by a 2 hour lab period.
Running MrBayes on the cluster
First, login to bbcsrv3.biotech.uconn.edu and upload the go.nex and nylander.nex files.
Second, use the mkdir command to create a directory named mbpart, and use the mv command to move go.nex and nylander.nex into that directory:
mkdir mbpart mv go.nex mbpart mv nylander.nex mbpart
Third, create (in this newly-created mbpart directory) a file named runmb.sh that looks like this:
#$ -S /bin/bash #$ -cwd #$ -m ea #$ -M change.me@uconn.edu #$ -N nylander mb go.nex
Be sure to change the email address! Otherwise some person at UConn named Change Me will be getting a lot of strange emails!
Feel free to also change the job name. I chose nylander as the name of the job, but you may want to see something else showing up as the name of the job when the email comes in (or when you use qstat to check on your run).
Fourth, cd into the mbpart directory and start the run using the qsub command:
cd mbpart qsub runmb.sh
You can periodically check the status of your run using
qstat
You will find the output files that MrBayes generates in the mbpart directory.
Analyzing the output
Try to answer these questions based on the file output.txt. As usual, you can peek at my answer by hovering over the "answer" link.
- Find the section labeled "Active parameters" Can you tell from this table that separate gamma shape parameters will be used for 18S and COI genes? answer
- Can you tell that the same topology will be applied to all three partition subsets? answer
- Why is there a warning that "There are 25 characters incompatible with the specified coding bias"? answer
- What is the log of the harmonic mean of the likelihood for this model? (write this down for later reference) answer
- What is the AT content (sum of the nucleotide frequencies of A and T) in the COI gene? answer
- Which subset of characters evolves the fastest on average? Which evolves most slowly? (hint: look at the subset relative rate parameters m{1}, m{2} and m{3}) answer
- Approximately how much faster does a typical morphological character evolve compared to a typical 18S site? answer
- Why does the simple average of the three relative rates equal 1.64 and not 1.0? answer
Now open Tracer and load your nylander.nex.p file into the program. Click on the Trace tab to see a plot of parameter values against State (which is how Tracer refers to the generation or iteration).
- On the left, in the ESS (Effective Sample Size) column, are any values red (<100) or yellow (<200)? answer
- Looking at the trace plot, can you suggest something you might do in a future run to increase the EES of this parameter? answer
- On the left, select m{1}, m{2} and m{3} at the same time (hold down the shift key as you click them), then click the "Marginal Prob Distribution" tab and, finally, use the "Legend" drop-down control to place a legend at the upper right. Which of the 3 subset relative rates are you least certain about (i.e. has the largest marginal posterior variance) answer
- Now do the same for pi(A){3}, pi(C){3}, pi(G){3}, and pi(T){3}. This should make the AT bias at the COI gene clear.
Using the marginal likelihood to choose a model
In your first run, you wrote down the harmonic mean of the likelihoods sampled during the MCMC analysis. This value is an estimate of the (log of the) marginal likelihood (the denominator on the right side of Bayes' Rule). It turns out that the harmonic mean estimate is always an overestimate of the quantity it is supposed to be estimating, and a variety of better ways of estimating marginal likelihoods have been invented recently. MrBayes provides one of these better methods, known as the stepping-stone method, which you have heard (will hear) about in lecture.
Why estimate the marginal likelihood, you ask? The marginal likelihood turns out to be one of the primary ways to compare models in Bayesian statistics. In the Bayesian framework, the effects of the prior have to be included because model performance is affected by the choice of prior distributions: if you choose a prior that presents an opinion very different than the opinion provided by your data, the resulting tug-of-war between prior and likelihood must somehow be reflected in the criterion you are using to choose a model. If you use AIC or BIC to choose a model, you are only getting the opinion of the data because these methods (as well as likelihood ratio tests) base their results only on the peak of the likelihood curve and the number of estimated parameters.
The marginal likelihood is a weighted average of the likelihood over all combinations of parameter values allowed by the prior. The weights for the weighted average are provided by the prior. Thus, a model will do very well if both prior and likelihood are high for the same parameter combinations, and will be lower for models in which the prior is high where the likelihood is low, or vice versa.
Estimating the marginal likelihood using the stepping-stone method
Let's ask MrBayes to estimate the marginal likelihood using the stepping-stone method, and then compare that estimate with the one provided by the harmonic mean method. Like likelihoods, marginal likelihoods are always used on the log scale, so whenever I say marginal likelihood I probably meant to say log marginal likelihood. We need to make very few changes to our MrBayes block to perform a stepping-stone analysis.
First, copy your go.nex file into a new directory so that this run will not overwrite files from your previous run: I've chosen to call the new directory mbss, but you are free to use any name you like:
cd # this will take you back to your home directory mkdir mbss # create a new directory cp mbpart/go.nex mbss # copy go.nex to the new directory cp mbpart/nylander.nex mbss # copy the data file to the new directory cp mbpart/runmb.sh mbss # copy the qsub script into the new directory cd mbss # move into the new directory
Second, replace your existing mcmc command in go.nex with the following two commands:
mcmc ngen=1100000 samplefreq=100 printfreq=10000 nchains=1 nruns=1; ss alpha=0.3 nsteps=10;
The only thing I've done to the mcmc command is increase ngen from 1000000 up to 1100000 and reduce samplefreq from 1000 down to 100.
Go ahead and submit this to the cluster:
qsub runmb.sh
MrBayes is now running an MCMC analysis that begins exploring the posterior distribution but ends up exploring the prior distribution. The target distribution changes in a series of steps. The name stepping-stone arises from a stream-crossing metaphor: if a stream is too wide to jump, you can keep your feet dry by making smaller jumps to successive "stepping stones" until the stream is crossed. In marginal likelihood estimation, we are trying to estimate the area under the posterior kernel (posterior kernel is statistical jargon for unnormalized posterior density). We know that the area under the prior density is 1, so if we estimated the ratio of the area under the posterior kernel to the area under the prior, that would be identical to the marginal likelihood. Unfortunately, there is a huge difference between these two areas, and the ratio is thus difficult to estimate directly. Instead we estimate a series of ratios that, when multiplied together, equal the desired ratio. These intermediate ratios represent smaller differences and are thus easier to estimate accurately. To estimate these "stepping-stone" ratios, MrBayes needs to obtain samples from distributions intermediate bewteen the prior and posterior.
MrBayes will, in our case, divide the 11000 samples (1100000 generations divided by 100 generations/sample) by 11 steps to yield 1000 samples per step. This is a little confusing because we specified nsteps=10, not nsteps=11. By default, MrBayes uses the first step as burnin, so you need to specify ngen and samplefreq in such a way that you get the desired number of samples per step. The formula is ngen = (nsteps+1)*(samplefreq)*(samples/step). In our case, ngen = (10+1)*(100)*(1000) = 1100000.
Spacing the stepping stones
The setting alpha=0.3 has to do with how evenly spaced the stepping-stones are placed in the stream: if alpha were set to 1, the beta values used to modify the likelihood would all be the same distance apart. This does not translate into evenly-spaced stepping stones however, and setting alpha to be smaller than 1 usually results in more evenly spaced stones and thus more accurate estimates of ratios close to the prior end of the spectrum.
Interpreting the results
Once the run finishes, try to answer the following questions based on what you find in the outout.txt file:
- What is the estimated log marginal likelihood using the stepping-stone method? Search for "Marginal likelihood (in natural log units) estimated using stepping-stone sampling..." answer
- How does this estimate compare to that obtained using the harmonic mean approach? answer
Assuming that the stepping-stone estimate is closer to reality, it is clear that the harmonic mean estimator greatly overestimates how well the model is performing.
Challenge
Your challenge for the last part of the lab is to estimate the marginal likelihood using the stepping-stone method for a "combined" model that partitions the data into only 2 subsets: morphology (1-166) and molecular (167-2397). You should create a new directory for this so that you do not overwrite files you've already created.
- What is the log marginal likelihood for this "combined" partition scheme? answer
- Based on marginal likelihoods, is it better to divide the molecular data into separate 18S and COI subsets, or is it better to treat them as one combined subset? answer
- Assuming you found that the 3-subset partition scheme is better than the 2-subset partitioning, why do you think applying a separate model to 18S and COI improves the marginal likelihood? answer
That's it for today
This has been an unusual lab because we have not even looked at any phylogenetic trees resulting from these analyses! My purpose here is to show you how to set up a partitioned run with a mixture of morphological characters and sequence data, and how to estimate the marginal likelihood for a model accurately using the stepping-stone method. The original paper is worth reading if you end up running your own Bayesian analysis of combined morphological and molecular data. Nylander et al. do a great job of discussing the many issues that arise from partitioning the data and combining morphological characters with DNA sequences, and you should now have the background to understand a paper like this. The stepping-stone method is described in this paper.