Difference between revisions of "Phylogenetics: Likelihood Lab"
Paul Lewis (Talk | contribs) |
Paul Lewis (Talk | contribs) (→Likelihood ratio tests) |
||
| (11 intermediate revisions by the same user not shown) | |||
| Line 117: | Line 117: | ||
Now get PAUP* to show you the maximum likelihood estimates for the parameters of the F81 model used in this analysis (the 1 here refers to tree 1 in memory): | Now get PAUP* to show you the maximum likelihood estimates for the parameters of the F81 model used in this analysis (the 1 here refers to tree 1 in memory): | ||
lscores 1; | lscores 1; | ||
| − | + | <div style="background-color: #ddddff; padding: 5px;">What are the empirical base frequencies for this data set?</div> <!-- {{title|A is 0.27029, C is 0.21751 , G is 0.31106, and T is 0.20115|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the lnL of this tree under this "empirical base frequencies" version of the F81 model?</div> | |
| − | + | <!-- {{title|-3351.78855|answer}} --> | |
| + | <div style="background-color: #ddddff; padding: 5px;">What proportion of sites are constant? (The <tt>cstatus</tt> command will give you this information)</div> <!-- {{title|0.716304|answer}} --> | ||
=== Estimate base frequencies === | === Estimate base frequencies === | ||
| Line 125: | Line 126: | ||
lset basefreq=estimate; | lset basefreq=estimate; | ||
lscores 1; | lscores 1; | ||
| − | + | <div style="background-color: #ddddff; padding: 5px;">What are the maximum likelihood estimates (MLEs) of the base frequencies?</div> <!--{{title|A is 0.274492, C is 0.208950, G is 0.289193 and T is 0.227365|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the lnL of this tree under the "estimated base frequencies" version of the F81 model?</div> <!-- {{title|-3348.34075|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">How many parameters are being estimated using the F81 model?</div> <!-- {{title|16 total (3 base frequencies plus 13 branch lengths)|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">Is it better than the lnL under the "empirical base frequencies" version of the F81 model?</div> <!-- {{title|yes, -3348.34075 > -3351.78855|answer}} --> | |
=== Estimate transition/transversion bias === | === Estimate transition/transversion bias === | ||
| Line 134: | Line 135: | ||
lset nst=2 basefreq=estimate tratio=estimate; | lset nst=2 basefreq=estimate tratio=estimate; | ||
lscores 1; | lscores 1; | ||
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the MLE of the transition/transversion ratio under the HKY85 model?</div> <!-- {{title|1.888808|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the MLE of the transition/transversion ''rate'' ratio under the HKY85 model?</div> <!-- {{title|3.715051|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the lnL of this tree under the HKY85 model?</div> <!-- {{title|-3268.85606|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">How many parameters are being estimated using the HKY85 model?</div> <!-- {{title|17 total (3 base frequencies, 1 rate ratio and 13 branch lengths)|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">Does the HKY model fit the data better than the F81 model?</div> <!-- {{title|yes, -3268.85606 > -3348.34075|answer}} --> | |
| − | + | <!-- Can you explain the difference between the transition/transversion ratio and the transition/transversion rate ratio? --> | |
| − | + | ||
| − | + | ||
=== Estimate the proportion of invariable sites === | === Estimate the proportion of invariable sites === | ||
Now ask PAUP* to estimate pinvar, the proportion of invariable sites, using the command <tt>lset pinvar=estimate</tt>. The HKY85 model with among-site rate heterogeneity modeled using the two-category invariable sites approach is called the HKY85+I model. | Now ask PAUP* to estimate pinvar, the proportion of invariable sites, using the command <tt>lset pinvar=estimate</tt>. The HKY85 model with among-site rate heterogeneity modeled using the two-category invariable sites approach is called the HKY85+I model. | ||
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the MLE of pinvar under the HKY85+I model?</div> <!-- {{title|0.633121|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">Is the MLE of pinvar larger or smaller than the proportion of constant sites?</div> <!-- {{title|smaller, 0.633121 < 0.716304|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">Why are these two proportions different? That is, how can a site be constant but not invariable?</div> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the lnL of this tree under the HKY85+I model?</div> <!-- {{title|-3174.72872|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">How many parameters are being estimated using the HKY85+I model?</div> <!-- {{title|18 total (3 base frequencies, 1 rate ratio, 1 proportion of invariable sites and 13 branch lengths)|answer}} --> | |
=== Estimate the heterogeneity in rates among sites === | === Estimate the heterogeneity in rates among sites === | ||
| Line 157: | Line 156: | ||
lscores 1; | lscores 1; | ||
The HKY85 model with among-site rate heterogeneity modeled using the discrete gamma approach is called the HKY85+G model. | The HKY85 model with among-site rate heterogeneity modeled using the discrete gamma approach is called the HKY85+G model. | ||
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the MLE of the gamma shape parameter under the HKY85+G model?</div> <!-- {{title|0.260778|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the lnL of this tree under the HKY85+G model?</div> <!-- {{title|-3171.55074|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">How many parameters are being estimated using the HKY85+G model?</div> <!-- {{title|18 total (3 base frequencies, 1 rate ratio, 1 gamma shape and 13 branch lengths)|answer}} --> | |
=== Estimate both pinvar and the gamma shape parameter === | === Estimate both pinvar and the gamma shape parameter === | ||
| − | Now | + | Now ask PAUP* to estimate both pinvar and the gamma shape parameter simultaneously (the HKY85+I+G model). |
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the MLE of the gamma shape parameter under the HKY85+I+G model?</div> <!-- {{title|0.411387|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the MLE of the pinvar parameter under the HKY85+I+G model?</div> <!-- {{title|0.222433|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">Is the MLE of the shape parameter higher or lower under the HKY85+I+G model compared to the HKY85+G model? Explain why this is so.</div> <!-- {{title|higher, 0.411387 > 0.260778|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the lnL of this tree under the HKY85+I+G model?</div> <!-- {{title|-3171.49320|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">How many parameters are being estimated using the HKY85+I+G model?</div> <!-- {{title|19 total (3 base frequencies, 1 rate ratio, 1 proportion of invariable sites, 1 gamma shape and 13 branch lengths)|answer}} --> | |
== Likelihood ratio tests== | == Likelihood ratio tests== | ||
| Line 178: | Line 177: | ||
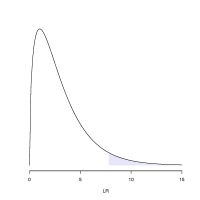
To be specific, we would like to know whether LR falls inside the 5% right tail of the chi-squared distribution (see figure to the right for an example). If it does, then it should be considered an unusually large value of LR; i.e. not a LR value that would normally arise (95% of the time) if the models were equivalent explanations of the data. We can use R to do the calculation for us. As with PAUP*, the default version of R is old, so load a recent version and start it(<tt>module avail</tt> will show you all available versions of all available software if you are curious): | To be specific, we would like to know whether LR falls inside the 5% right tail of the chi-squared distribution (see figure to the right for an example). If it does, then it should be considered an unusually large value of LR; i.e. not a LR value that would normally arise (95% of the time) if the models were equivalent explanations of the data. We can use R to do the calculation for us. As with PAUP*, the default version of R is old, so load a recent version and start it(<tt>module avail</tt> will show you all available versions of all available software if you are curious): | ||
| − | module load R/3. | + | module load R/3.6.1 |
R | R | ||
| − | Suppose LR = 6.91 and d.f. = 1 (one parameter differs between the models). To ask R to tell us what fraction of the 1 d.f. chi-square distribution is to the left of 6.91, use the pchisq (chi-squared cumulative probability) command: | + | Suppose LR = 6.91 (the difference in log likelihood between the models is 3.455) and d.f. = 1 (one parameter differs between the models). To ask R to tell us what fraction of the 1 d.f. chi-square distribution is to the left of 6.91, use the pchisq (chi-squared cumulative probability) command: |
pchisq(6.91, df=1) | pchisq(6.91, df=1) | ||
You should get this response | You should get this response | ||
| Line 199: | Line 198: | ||
You should have all the numbers you need to perform these likelihood ratio tests. If, however, you have not written some of them down, and thus need to redo some of these analyses, you might need to know how to "turn off" rate heterogeneity using the following command: | You should have all the numbers you need to perform these likelihood ratio tests. If, however, you have not written some of them down, and thus need to redo some of these analyses, you might need to know how to "turn off" rate heterogeneity using the following command: | ||
lset rates=equal pinvar=0; | lset rates=equal pinvar=0; | ||
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the likelihood ratio test statistic for F81 vs. HKY85?</div> <!-- {{title|158.9694|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">How many degrees of freedom for this test?</div> <!-- {{title|1|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">What is the significance (P-value) for this test?</div> <!-- {{title|0.0|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">Does allowing for a transition/transversion bias make a significant difference?</div> <!-- {{title|yes|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">Does the HKY85+I model explain the data signficantly better than an equal rates HKY85 model?</div> <!-- {{title|yes|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">Does the HKY85+G model explain the data signficantly better than an equal rates HKY85 model?</div> <!-- {{title|yes|answer}} --> | |
| − | + | <div style="background-color: #ddddff; padding: 5px;">Does the HKY85+I+G model explain the data signficantly better than either HKY85+I or HKY85+G alone?</div> <!-- {{title|I+G signif. better than I alone but not better than G alone|answer}} --> | |
| − | + | ||
Using the simplest model that you can defend (of the five we have examined: F81, HKY85, HKY85+I, HKY85+G, HKY85+I+G), perform an heuristic search under the maximum likelihood criterion. To make the analysis go faster, we will ask PAUP* to '''not''' re-estimate all the model parameters for every tree it examines during the search. To do this, first use the <tt>lset</tt> command to set up the model you are planning to use. Use the <tt>lscores</tt> command to force PAUP* to re-estimate all of the parameters of your selected model on some tree (the tree just needs to be something reasonable, such as a NJ tree or the F81 tree you have been using). Now, for every parameter that you estimated, change the word <tt>estimate</tt> to <tt>previous</tt> in the <tt>lset</tt> command, and after executing this new <tt>lset</tt> command, start a search using just <tt>hsearch</tt>. PAUP* will fix the parameters at the previous values (i.e. the estimates you just forced it to calculate) and use these same values for every tree examined during the search. | Using the simplest model that you can defend (of the five we have examined: F81, HKY85, HKY85+I, HKY85+G, HKY85+I+G), perform an heuristic search under the maximum likelihood criterion. To make the analysis go faster, we will ask PAUP* to '''not''' re-estimate all the model parameters for every tree it examines during the search. To do this, first use the <tt>lset</tt> command to set up the model you are planning to use. Use the <tt>lscores</tt> command to force PAUP* to re-estimate all of the parameters of your selected model on some tree (the tree just needs to be something reasonable, such as a NJ tree or the F81 tree you have been using). Now, for every parameter that you estimated, change the word <tt>estimate</tt> to <tt>previous</tt> in the <tt>lset</tt> command, and after executing this new <tt>lset</tt> command, start a search using just <tt>hsearch</tt>. PAUP* will fix the parameters at the previous values (i.e. the estimates you just forced it to calculate) and use these same values for every tree examined during the search. | ||
| − | + | <div style="background-color: #ddddff; padding: 5px;">Does the model you have selected place all the chlorophyll-b organisms together?</div> | |
This lab is already a bit long, so we will not take time to do it now, but I hope you realize that you could figure out exactly what parameter(s) are needed in the model to get this tree right. JC69 doesn't do it, nor does F81 (as you may have noticed), but it actually doesn't take much beyond JC69 to do the trick. | This lab is already a bit long, so we will not take time to do it now, but I hope you realize that you could figure out exactly what parameter(s) are needed in the model to get this tree right. JC69 doesn't do it, nor does F81 (as you may have noticed), but it actually doesn't take much beyond JC69 to do the trick. | ||
Latest revision as of 19:38, 3 February 2020

|
EEB 5349: Phylogenetics |
Contents
- 1 Goals
- 2 Getting started
- 3 Download the data file algae.nex
- 4 Obtain the maximum likelihood tree under the F81 model
- 5 Estimate base frequencies
- 6 Estimate transition/transversion bias
- 7 Estimate the proportion of invariable sites
- 8 Estimate the heterogeneity in rates among sites
- 9 Estimate both pinvar and the gamma shape parameter
- 10 Likelihood ratio tests
- 11 Literature Cited
Goals
The goal of this lab exercise is to show you how to conduct maximum likelihood analyses in PAUP* using several models, and to decide among competing models using likelihood ratio tests.
Getting started
Login to your account on the Health Center (Xanadu) cluster (ssh username@xanadu-submit-ext.cam.uchc.edu). Type the following:
srun --qos=general --pty bash
to start a session on a node that is not currently running jobs. Once you see the prompt, type
module load paup/4.0a-166
to load the paup module.
Download the data file algae.nex
Download the data file algae.nex using the following curl command on the cluster:
curl -O http://hydrodictyon.eeb.uconn.edu/people/plewis/courses/phylogenetics/data/algae.nex
If you remember from lecture, adding more parameters to a model to account for different aspects of nucleotide and sequence evolution can -- but does not necessarily -- improve the explanatory ability of a model, or its ability to produce a correct phylogeny. Our goal for this lab will be to see if we can tease apart which aspects of sequence evolution are most important for getting the tree correct. The accepted phylogeny (based on much evidence besides these data) places all the chlorophyll-b-containing plastids together (Lockhart, Steel, Hendy, and Penny, 1994). Thus, there should be a branch in the tree separating all taxa from the two that do not have chlorophyll b, namely the cyanobacterium Anacystis (which has chlorophyll a and phycobilin accessory pigments) and the chromophyte Olithodiscus (which has chlorophylls a and c).
Obtain the maximum likelihood tree under the F81 model
The first goal is to learn how to obtain maximum likelihood estimates of the parameters in several different substitution models. Use PAUP* to answer the following questions. Start by obtaining the maximum likelihood tree under the F81 model. Create a run.nex file and save in it the following:
#nexus begin paup; execute algae.nex; set criterion=likelihood; lset nst=1 basefreq=empirical; hsearch; end;
The nst=1 tells PAUP* that we want a model having just one substitution rate parameter (the JC69 and F81 models both fall in this category). The basefreq=empirical tells PAUP* that we want to use simple estimates of the base frequencies. The empirical frequency of the base G, for example, is the value you would get if you simply counted up all the Gs in your entire data matrix and divided by the total number of nucleotides. The empirical frequencies are not usually the same as the maximum likelihood estimates (MLEs) of the base frequencies, but they are quick to calculate and often very close to the corresponding MLEs.
Execute run.nex in PAUP* and issue the following command to show the tree:
showtrees;
One problem is that the tree is drawn in such a way that it appears to be rooted within the flowering plants (tobacco and rice). Specifying the cyanobacterium Anacystis as the outgroup makes more sense biologically:
outgroup Anacystis_nidulans; [could also use "outgroup 7" because Anacystis is the 7th (of 8) taxa in the data matrix] showtrees;
The edge lengths are not proportional to the expected number of substitutions when using the showtrees command. To fix this, use the describetrees command rather than the simpler showtrees command:
descr 1 / plot=phylogram;
As with all PAUP* commands, it is usually not necessary to type the entire command name, only enough letters that PAUP* can determine unambiguously which command you want. Here, you typed descr instead of describetrees, and it worked just fine.
You will be working with this tree for quite awhile. Resist the temptation to do heuristic searches with each model, as it will be important to compare the performance of all of the models on the same tree topology! To be safe, save this tree to a file named f81.tre using the savetrees command:
savetrees file=f81.tre brlens;
If you ever need to read this tree back in, use the gettrees command:
gettrees file=f81.tre;
Now get PAUP* to show you the maximum likelihood estimates for the parameters of the F81 model used in this analysis (the 1 here refers to tree 1 in memory):
lscores 1;
Estimate base frequencies
Now estimate the base frequencies on this tree with maximum likelihood as follows. Note how the lscores command is used to force PAUP* to recompute the likelihood (under the revised model) and spit out the parameter estimates.
lset basefreq=estimate; lscores 1;
Estimate transition/transversion bias
Switch to the HKY85 model now and estimate the transition/transversion ratio along with the base frequencies. The way you specify the HKY model in PAUP* is to tell it you want a model with 2 substitution rate parameters (nst=2), and that you want to estimate the base frequencies (basefreq=estimate) and the transition/transversion ratio (tratio=estimated). Note that these specifications also apply to the F84 model, so if you want PAUP* to use the F84 model, you would need to add variant=f84 to the lset command.
lset nst=2 basefreq=estimate tratio=estimate; lscores 1;
Estimate the proportion of invariable sites
Now ask PAUP* to estimate pinvar, the proportion of invariable sites, using the command lset pinvar=estimate. The HKY85 model with among-site rate heterogeneity modeled using the two-category invariable sites approach is called the HKY85+I model.
Estimate the heterogeneity in rates among sites
Now set pinvar=0 and tell PAUP* to use the discrete gamma distribution with 5 rate categories. Here are the commands for doing this all in one step:
lset pinvar=0 rates=gamma ncat=5 shape=estimate; lscores 1;
The HKY85 model with among-site rate heterogeneity modeled using the discrete gamma approach is called the HKY85+G model.
Estimate both pinvar and the gamma shape parameter
Now ask PAUP* to estimate both pinvar and the gamma shape parameter simultaneously (the HKY85+I+G model).
Likelihood ratio tests
In this section, you will perform some simple likelihood ratio tests to decide which of the models used in the previous section does the best job of explaining the data while keeping the number of parameters used to a minimum.
Determining significance
A model having k parameters can always attain a higher likelihood than any model having fewer than k parameters that is nested within it (you should be able to explain why this is true), so the question we will be asking is whether more complex (i.e. more parameter-rich) models fit significantly better than simpler nested models. To do this we will assume that the likelihood ratio test statistic LR (equal to twice the difference in log-likelihoods) has the same distribution as a chi-squared random variable with degrees of freedom (d.f.) equal to the difference in the number of estimated parameters in the two models. (A parameter whose value is fixed doesn't count as a parameter.)
To be specific, we would like to know whether LR falls inside the 5% right tail of the chi-squared distribution (see figure to the right for an example). If it does, then it should be considered an unusually large value of LR; i.e. not a LR value that would normally arise (95% of the time) if the models were equivalent explanations of the data. We can use R to do the calculation for us. As with PAUP*, the default version of R is old, so load a recent version and start it(module avail will show you all available versions of all available software if you are curious):
module load R/3.6.1 R
Suppose LR = 6.91 (the difference in log likelihood between the models is 3.455) and d.f. = 1 (one parameter differs between the models). To ask R to tell us what fraction of the 1 d.f. chi-square distribution is to the left of 6.91, use the pchisq (chi-squared cumulative probability) command:
pchisq(6.91, df=1)
You should get this response
[1] 0.9914285
which tells us that 99.14285% of the distribution is to the left of 6.91 and thus less than 1% is to the right, which means 6.91 is significantly large (because the probability of seeing a value that large or larger is less than 5%).
To find the critical value, you can use the qchisq (chi-squared quantile) command:
qchisq(0.95, df=1)
This tells us the specific value that we have to exceed in order to be significant. In this case (when d.f.=1), it is 3.841459.
What parameters make the fit of the model significantly better?
The model with which we will begin is the F81 model with estimated base freqencies. Compare this F81 model to the HKY85 model, which differs from the F81 model only in the fact that it allows transitions and transversions to occur at different rates.
To calculate the likelihood ratio test statistic LR, subtract the log-likelihood of the less complex model from that of the more complex model and multiply by 2. This will give you a positive number. If you ever get a negative LR statistic, it means you have the models in the wrong order.
You should have all the numbers you need to perform these likelihood ratio tests. If, however, you have not written some of them down, and thus need to redo some of these analyses, you might need to know how to "turn off" rate heterogeneity using the following command:
lset rates=equal pinvar=0;
Using the simplest model that you can defend (of the five we have examined: F81, HKY85, HKY85+I, HKY85+G, HKY85+I+G), perform an heuristic search under the maximum likelihood criterion. To make the analysis go faster, we will ask PAUP* to not re-estimate all the model parameters for every tree it examines during the search. To do this, first use the lset command to set up the model you are planning to use. Use the lscores command to force PAUP* to re-estimate all of the parameters of your selected model on some tree (the tree just needs to be something reasonable, such as a NJ tree or the F81 tree you have been using). Now, for every parameter that you estimated, change the word estimate to previous in the lset command, and after executing this new lset command, start a search using just hsearch. PAUP* will fix the parameters at the previous values (i.e. the estimates you just forced it to calculate) and use these same values for every tree examined during the search.
This lab is already a bit long, so we will not take time to do it now, but I hope you realize that you could figure out exactly what parameter(s) are needed in the model to get this tree right. JC69 doesn't do it, nor does F81 (as you may have noticed), but it actually doesn't take much beyond JC69 to do the trick.
Literature Cited
Lockhart, P. J., Steel, M. A., Hendy, M. D., & Penny, D. (1994). Recovering evolutionary trees under a more realistic model of sequence evolution. Molecular Biology and Evolution, 11(4), 605–612.