Phylogenetics: BayesTraits Lab

|
EEB 349: Phylogenetics |
| In this lab you will learn how to use the program BayesTraits, written by Andrew Meade and Mark Pagel. BayesTraits can perform several analyses related to evaluating evolutionary correlation and ancestral state reconstruction in discrete morphological traits. This program is meant to replace the older programs Discrete and Multistate. In this lab, you will download and use BayesTraits entirely on your own laptop. |
Contents
Download BayesTraits
Download BayesTraits from Mark Pagel's web site, click on the "Software" link, then click on the "Description and Downloads" link under "BayesTraits". Download the version specific to your platform. BayesTraits will unpack itself to a folder containing the program itself along with several tree and data files (e.g. Primates.txt and Primates.trees). I will hereafter refer to the folder containing these files as simply the BayesTraits folder. Go back to Mark Pagel's web site and download the manual for BayesTraits. This is a PDF file and should open in your browser window.
Download the tree and data files
For this exercise, you will use data and trees used in the SIMMAP analyses presented in this paper (you should recognize the names of at least two of the authors of this paper):
Jones C.S., Bakker F.T., Schlichting C.D., Nicotra A.B. 2009. Leaf shape evolution in the South African genus Pelargonium L'Her. (Geraniaceae). Evolution. 63:479–497.
The data and trees were not made available in the online supplementary materials for this paper, but I have obtained permission to use them for this laboratory exercise. The links below are password-protected, so ask us for the username and password before clicking on the links:
- pelly.txt This is the data file. It contains data for two traits (see below) for 154 taxa in the plant genus Pelargonium.
- pelly.tre This is the tree file. It contains 99 trees sampled from an MCMC analysis of DNA sequences.
You should move these files to the aforementioned BayesTraits folder so that they can be easily found by the BayesTraits program.
Assessing the strength of association between two binary characters
The first thing we will do is see if the two characters (leaf dissection and leaf venation) in pelly.txt are evolutionarily correlated.
Trait 1: Leaf dissection
The leaf dissection trait comprises two states (I've merged some states in the original data matrix to produce just 2 states):
- 0 means leaves are entire (unlobed or shallowly lobed in the original study), and
- 1 means leaves are dissected (lobed, deeply lobed, or dissected in the original study).
Trait 2: Leaf venation
The leaf venation trait comprises two states:
- 0 means leaves are pinnately veined (one main vein runs down the long axis of the leaf blade), and
- 1 means leaves are palmately veined (several major veins meet at the base of the leaf).
To test whether these two traits are correlated, we will estimate the marginal likelihood under two models. The independence model assumes that the two traits are uncorrelated. The dependence model allows the two traits to be correlated in their evolution. The model with the higher marginal likelihood will be the preferred model. You will recall that we discussed both of these models in lecture, and also discussed the stepping-stone method that BayesTraits uses to evaluate models. You may wish to pull up those lectures to help answer the questions that you will encounter momentarily, as well as the BayesTraits manual.
Maximum Likelihood: Independence model
If you are using Windows, start BayesTraits by opening a console window , navigate to the BayesTraits directory, and type the following to start the program:
BayesTraitsV2 pelly.tre pelly.txt
If you are using a Mac, start BayesTraits by opening a terminal window, navigate to the BayesTraits directory, and type the following to start the program:
./BayesTraitsV2 pelly.tre pelly.txt
You should see this selection appear:
Please select the model of evolution to use. 1) MultiState 2) Discrete: Independent 3) Discrete: Dependant 4) Continuous: Random Walk (Model A) 5) Continuous: Directional (Model B) 6) Continuous: Regression 7) Independent Contrast 8) Independent Contrast: Correlation 9) Independent Contrast: Regression 10) Discrete: Covarion
Press the 2 key to select the Independent model. Now you should see these choices appear:
Please Select the analysis method to use. 1) Maximum Likelihood. 2) MCMC
Press the 1 key to select maximum likelihood. Now you should see some output showing the choices you explicitly (or implicitly) made:
Options:
Model: Discete Independant
Tree File Name: pelly.tre
Data File Name: pelly.txt
Log File Name: pelly.txt.log.txt
Summary: False
Seed 3162959925
Analsis Type: Maximum Likelihood
ML attempt per tree: 10
Precision: 64 bits
Cores: 1
No of Rates: 4
Base frequency (PI's) None
Character Symbols: 00,01,10,11
Using a covarion model: False
Restrictions:
alpha1 None
beta1 None
alpha2 None
beta2 None
Tree Information
Trees: 99
Taxa: 154
Sites: 1
States: 4
Now type run to perform the analysis, which will consist of estimating the parameters of the independent model on each of the 99 trees contained in the pelly.tre file.
Tree No Lh alpha1 beta1 alpha2 beta2 Root - P(0,0) Root - P(0,1) Root - P(1,0) Root - P(1,1) 1 -157.362972 53.767527 34.523176 35.319157 20.707416 0.249998 0.250002 0.249998 0.250002 2 -158.179984 53.313539 34.182683 36.038859 20.997536 0.249999 0.250001 0.249999 0.250001 . . . 98 -156.647307 52.357626 36.749282 27.270771 13.086248 0.250244 0.249756 0.250244 0.249756 99 -156.532925 52.321467 36.641688 27.402067 13.200124 0.250234 0.249767 0.250233 0.249766
You will notice that BayesTraits created a new file: pelly.txt.log.txt. Rename this file ml-independant.txt so that it will not be overwritten the next time you run BayesTraits.
Try to answer these questions using the output you have generated (ask us if anything doesn't make sense):
- Which occurs at a faster rate: pinnate to palmate, or palmate to pinnate? answer
- Which occurs at a faster rate: entire to dissected, or dissected to entire? answer
- What do you think Root - P(1,1) means (i.e. the last column of numbers)? answer
Maximum Likelihood: Dependence model
Run BayesTraits again, this time typing 3 on the first screen to choose the dependence model and again typing 1 on the second screen to select maximum likelihood. You should see this output showing the options selected:
Options:
Model: Discete Dependent
Tree File Name: pelly.tre
Data File Name: pelly.txt
Log File Name: pelly.txt.log.txt
Summary: False
Seed 3601265953
Analsis Type: Maximum Likelihood
ML attempt per tree: 10
Precision: 64 bits
Cores: 1
No of Rates: 8
Base frequency (PI's) None
Character Symbols: 00,01,10,11
Using a covarion model: False
Restrictions:
q12 None
q13 None
q21 None
q24 None
q31 None
q34 None
q42 None
q43 None
Tree Information
Trees: 99
Taxa: 154
Sites: 1
States: 4
Here is an example of the output produced after you type run to start the analysis:
Tree No Lh q12 q13 q21 q24 q31 q34 q42 q43 Root - P(0,0) Root - P(0,1) Root - P(1,0) Root - P(1,1) 1 -151.930254 66.451053 37.783888 0.000000 62.220033 23.997490 23.299393 46.110432 36.632979 0.24999 0.249981 0.250026 0.250000 2 -152.925691 67.152271 38.611193 0.000000 60.925185 24.514488 23.937433 45.313366 37.199310 0.24999 0.249983 0.250023 0.250001 . . . 98 -150.816306 36.534843 27.359325 0.000000 66.563262 19.823546 24.944519 63.940577 31.074092 0.250048 0.249750 0.250304 0.249898 99 -150.712705 37.316351 27.260833 0.000000 64.364694 20.107653 25.004246 60.945163 31.658536 0.250030 0.249779 0.250272 0.249919
Before doing anything else, rename the file pelly.txt.log.txt to ml-dependant.txt so that it will not be overwritten the next time you run BayesTraits.
Try to answer these questions using the output you have generated:
- What type of joint evolutionary transitions seem to often have very low rates (look for an abundance of zeros in a column)? answer
- What type of joint evolutionary transitions seem to often have very high rates (look for columns with rates in the hundreds)? answer
Bayesian MCMC: Dependence model
Run BayesTraits again, typing 3 on the first screen to choose the dependence model and this time typing 2 on the second screen to select MCMC. You should see this output showing the options selected:
Options:
Model: Discete Dependent
Tree File Name: pelly.tre
Data File Name: pelly.txt
Log File Name: pelly.txt.log.txt
Summary: False
Seed 3792635164
Precision: 64 bits
Cores: 1
Analysis Type: MCMC
Sample Period: 1000
Iterations: 1010000
Burn in: 10000
MCMC ML Start: False
Schedule File: pelly.txt.log.txt.Schedule.txt
Rate Dev: AutoTune
No of Rates: 8
Base frequency (PI's) None
Character Symbols: 00,01,10,11
Using a covarion model: False
Restrictions:
q12 None
q13 None
q21 None
q24 None
q31 None
q34 None
q42 None
q43 None
Prior Information:
Prior Categories: 100
q12 uniform 0.00 100.00
q13 uniform 0.00 100.00
q21 uniform 0.00 100.00
q24 uniform 0.00 100.00
q31 uniform 0.00 100.00
q34 uniform 0.00 100.00
q42 uniform 0.00 100.00
q43 uniform 0.00 100.00
Tree Information
Trees: 99
Taxa: 154
Sites: 1
States: 4
Before typing run type the following command, which tells BayesTraits to change all priors from the default Uniform(0,100) to an Exponential distribution with mean 30:
pa exp 30
Also type the following to ask BayesTraits to perform a stepping-stone analysis:
stones 100 10000
This will estimate 100 ratios to brook the gap between posterior and prior, using a sample size of 10000 for each "stone". Here is an example of the output produced after you type run to start the analysis:
Iteration Lh Harmonic Mean Tree No q12 q13 q21 q24 q31 q34 q42 q43 Root - P(0,0) Root - P(0,1) Root - P(1,0) Root - P(1,1) 11000 -155.195365 -155.195365 78 14.423234 34.800270 8.845985 45.927148 12.622435 50.476188 52.844895 32.149168 0.250068 0.249969 0.249994 0.249968 12000 -154.161705 -154.806538 82 64.601017 12.382781 9.259134 51.796365 12.002095 23.744903 30.316089 21.865930 0.249936 0.249957 0.250095 0.250012 . . . 1009000 -154.343996 -158.180036 30 33.555198 50.086092 11.294490 38.518607 24.461032 47.295157 43.477964 21.726938 0.250057 0.249939 0.250045 0.249959 1010000 -154.195259 -158.179054 87 29.584898 35.410909 2.003582 61.981073 16.976124 14.895266 49.111354 14.419644 0.251115 0.247854 0.252551 0.248480
Before doing anything else, rename the file pelly.txt.log.txt to mcmc-dependant.txt, and pelly.txt.log.Stones.txt to mcmc-dependant.Stones.txt so that they will not be overwritten the next time you run BayesTraits.
A couple of new columns have shown up in the output from the Bayesian analysis that were absent from the ML analysis output. The Harmonic Mean column provides a running estimate of the marginal likelihood. The fact that it is a running estimate means that the estimate is updated using each new sample so that the best estimate of the marginal likelihood from the entire run is provided on the last line of the output.
You will also notice that a column named 'Tree No is present that shows which of the 99 trees in the supplied pelly.tre> treefile was chosen at random to be used for that particular sample point. BayesTraits is trying to mimic sampling trees from the posterior distribution here; it cannot actually sample trees from the posterior because we have given it only data for two morphological characters, which would not provide nearly enough information to estimate the phylogeny for 154 taxa.
Try to answer these questions using the output you have generated:
- What is the estimated log marginal likelihood for this analysis? answer
- Based on the Bayesian Model Selection lecture, do you expect this to be an accurate estimate of the true log marginal likelihood? If not, is it an over- or and under-estimate? answer
Run BayesTraits again, this time specifying the Independent model, and again using MCMC and pa exp 30. Rename the output file from pelly.txt.log.txt to mcmc-independant.txt.
- What is the estimated log marginal likelihood for this analysis? answer
- Which is the better model according to these estimates of marginal likelihood? answer
Run BayesTraits again, specifying Dependent model, MCMC and, this time, specify the reversible-jump approach using the command rj exp 30. Type run to start, then when it finishes rename the output file rjmcmc-dependent.txt.
The reversible-jump approach carries out an MCMC analysis in which the number of model parameters (the dimension of the model) potentially changes from one iteration to the next. The full model allows each of the 8 rate parameters to be estimated separately, while other models restrict the values of some rate parameters to equal the values of other rate parameters. The output contains a column titled Model string that summarizes the model in a string of 8 symbols corresponding to the 8 rate parameters q12, q13, q21, q24, q31, q34, q42, and q43. For example, the model string "'1 0 Z 0 1 1 0 2" sets q21 to zero (Z), q13=q24=q42 (parameter group 0), q12=q31=q34 (parameter group 1), and q43 has its own non-zero value distinct from parameter groups 0 and 1.
You could copy the "spreadsheet" part of the output file into Excel and sort by the model string column, but let's instead use Python to summarize the output file. Download the file btsummary.py file and run it as follows:
python btsummary.py
This should produce counts of model strings. (If it doesn't, check to make sure your output file is named rjmcmc-dependent.txt because btsummary.py tries to open a file by that name.) Answer the following questions using the counts provided by btsummary.py.
- Which model string is most common? answer
- What does this model imply? answer
Notice that many (but not all) model strings have Z for q21. One way to estimate the marginal posterior probability of the hypothesis that q21=0 is to sum the counts for all model strings that have Z in that third position corresponding to q21. It is easy to modify btsummary.py to do this for us: open btsummary.py and locate the line containing the regular expression search that pulls out all the model strings from the BayesTrait output file:
model_list = re.findall("'[Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9]", stuff, re.M | re.S)
The re.findall function performs a regular expression search of the text stored in the variable stuff looking for strings that have a series of 8 space-separated characters, each of which is either the character Z or a digit between 0 and 9 (inclusive). Copy this line, then comment out one copy by starting the line with the hash (#) character. Now modify the other copy by forcing the regular expression search to look only for model strings having a Z in the third position:
#model_list = re.findall("'[Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9]", stuff, re.M | re.S)
model_list = re.findall("'[Z0-9] [Z0-9] [Z] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9]", stuff, re.M | re.S)
Rerun btsummary.py, and now the total matches should equal the number of model strings sampled in which q21=0.
- So what is the estimated marginal posterior probability that q21=0? answer
- Why is the term marginal appropriate here (as in marginal posterior probability)? answer
Estimating ancestral states
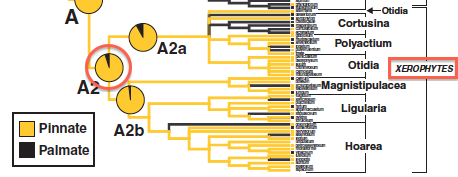
The Jones et al. 2009 study estimated ancestral states using SIMMAP. In particular, they found that the most recent common ancestor (MRCA) of the xerophytic (dry-adapted) clade of pelargoniums almost certainly had pinnate venation (see red circle in figure on right). Let's see what BayesTraits says.Start BayesTraits in the usual way, specifying 1 (Multistate) on the first screen and 2 (MCMC) on the second. After the options are output, type the following commands in, one line at a time, finishing with the run command:
pa exp 30 addmrca xero alternans104 rapaceum130 run
The addmrca command tells BayesTraits to add columns of numbers to the output that display the probabilities of each state for each character in the most recent common ancestor of the taxa listed (2 taxa are sufficient to define the MRCA, but more taxa may be included). The column headers for the last four columns of output should be
xero - S(0) - P(0) <-- character 0 (dissection), probability of state 0 (unlobed) xero - S(0) - P(1) <-- character 0 (dissection), probability of state 1 (dissected) xero - S(1) - P(0) <-- character 1 (venation), probability of state 0 (pinnate) xero - S(1) - P(1) <-- character 1 (venation), probability of state 1 (palmate)
- Which state is most common at the xerophyte MRCA node for leaf venation? answer
- Which state is most common at the xerophyte MRCA node for leaf dissection? answer
That concluded the introduction to BayesTraits. A glance through the manual will convince you that there is much more to this program than we have time to cover in a single lab period, but you should know enough now to explore the rest on your own if you need these features.